PARR: slicing method
After writing about PARR, I realized that the slicing method could be used, that I also used
for counting Hamiltonian cycles in product
graphs and generalized to finding all kinds of subgraphs in product graphs.
The idea is to take the PARR and slice it up into four by five points of the
PARR configuration up into four slices each containing two columns of four
points, and devise the rules for which the different configurations that can
occur in each slice connect. With this it is possible to construct a transition
matrix, and once this matrix is known, it is relatively easy to calculate the
number of PARR configurations with certain properties. I thought about
modifying the count.c
program, but decided that it was faster to implement it from scratch than try
to fit it in. A drawback is that I cannot calculate the recurrence equation for
the PARR's on four by n points, which would go beyond the original four
by five configurations. (I might decided to do this at a later point in time.)
I first used the program to verify the
results that I calculated before, and after this, I went on to calculate the
number of connected PARR configurations with the various conditions. The total
numbers of the results are presented in the table
below. Each cell in the table contains the number of total number of PARR
configurations and below it the number of connected configurations (in which
all points are connected to one of more connection). The first column gives
the PARR configurations where not all neighbour points have a connection. In
the second column the are always connected. The first row gives the PARR
configurations where crossing diagonals are allowed and the second column gives
the results for when they are not allowed. The bold number, is the number of
connected PARR configurations with no crossing diagonals and where not all
neighbour points need to have a connection. I assume that this the type of
PARR configurations that the original authors
had in mind.
| neighbours optional | neighbours connected |
| | crossing diagonals | 84,024,935,266,353,181
31,904,643,741,844,306 | 1,048,576
517,646 |
| no crossing diagonals | 4,147,603,839,035,069
847,157,460,556,451 | 2,976,416
2,041,600 |
The above count contain many configurations that are similar, except for
being translated, rotated, and/or mirror with the four by five points. Next
I will try to investigate the numbers of 'unique' PARR configurations.
(On September 16, I discovered that
numbers marked with red, are incorrect.)
Amsterdam
I went to Amsterdam with a friend. We visited the Stedelijk Museum Amsterdam. We first looked at some from before 1960,
including:
Next we watched the videos by Tromarama, a group of three artist from Indonesia. Then we looked at the
design exhibition in the reverse order. There we saw:
Next we walked through the second floor of the museum, where we saw, among
many others for which I cannot find the titles:
- Dead Magpie by Hamish Fulton.
- Eye level by Hamish Fulton.
- Drei Häuser mit Schlitzen, 1985 by Martin Kippenberger.
- Wooden House, 1976, by Andy Warhol.
- Man Walking on Runway, 1976, by Andy Warhol.
- TV-Buddha, 1974 by Nam June Paik.
- White Curve I, 1972, by Ellsworth Kelly.
- Blue Curve VI, 1982, by Ellsworth Kelly.
- cathedra, 1951 by Barnett Newman.
- Various sculptures by Wim T. Schippers.
In one of the rooms we also encountered: A year at the stedelijk: Tino Sehgal.
Finally, we went downstairs to visit the exhibition:
ZERO: Let us explore the stars about the ZERO movement. This contains works by Jan Schoonhoven.
My friend bought the catalogue for me. We saw
the Condensation Cube by Hans Haacke. I took a picture of Sphèr-Trames by
François Morellet showing a hexagon shape.
I also took a picture of Lichtrooster in de ruimte (light grid in
space) by Heinz Mack,
which for some magical reason reflected images rotated by about 90 degrees.
We also went to bookshop Scheltema, which
moved to Rokin 9. We mostly stayed at the top floor looking at second hand
and cheaply priced books. At 16:10, I purchased a black, hardback Moleskine
Daily Diary / Planner of 2016 (ISBN:8052204400010) for € 17.50.
Book
At 11:47:21, I bought the book De Aanslag (The Assault) by Harry Mulisch, ISBN:20150910114721, from bookshop Broekhuis for € 5.00.
In the evening, I visited The Gogbot festival
with a good friend. We first went to look at the exhibition at Concordia. We found NOVA EDEN by Rob van der Burg the most interesting. Next we looked inside
the 'Oude Kerk' and the sqaure around it. We found PHOTOTROPE by Pauline van Dongen most interesting. We did also have
a quick look in the TkkrLab dome, where it
was rather quiet. This year year lacked any very exciting instalations. Maybe
this is due to the theme: "The Internet of Things" with its focus on small,
often hidden, devices.
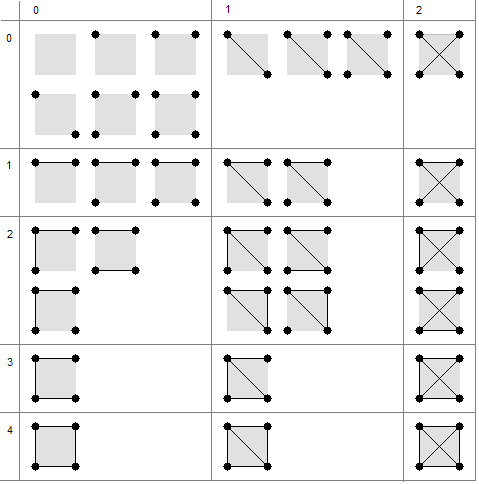
2 by 2 unique PARR configurations
I found a newspaper article Tussen kunst en wetenschap: Taco Stolk en de
schoonheid van wiskunde on page 15 of the Leidsch Dagblad of December 5, 2001. The text is not
completely visible, but I guess that PARR
stands for Particle Aesthetics Relation Research. With the article there is
also a picture of Taco Stolk sitting in front of laptop showing (with white on
a black background) a PARR configuration on seven points and nine connections
with two crossing diagonal connections. I conclude from this, that crossing
diagonals are allowed in PARR configurations.
Below, a drawing of all unique PARR configurations on a two by two grid, not
taking into account rotating and mirroring. I have placed them in rows and
columns depending on the number of horizontal and vertical connections (rows)
and the number of diagonal connections (columns). There are 31 of them:
Consciousness and the Brain
This morning, I finished reading
Consciousness and the Brain by
Stanislas
Dehaene, which I started reading on August 15. Two
months before, I bought it in Antwerp. The book is based on scientific
research in the past thirty years, which is reflected in list of references
covering 32 pages. Yet, the book is very readable and I enjoyed reading it.
There were only a few sections where I felt that the author was kind of
repeating the same statement in a different manner, probably with the aim to
clarify his central ideas. The book indeed exposes some very interesting
discoveries with respect to consciousness, but I doubt if those (now or in
the future) address the mystery with of subjective experience. I also think
that his ideas about how consciousness could (in the future) be achieve with
computers, rather simplistic, probably due to a lack of understandig of how
computers work.
Chapter 6 deals with the disorder of consciousness that can follow coma, such
as the vegetative and minimally conscious states. I wonder how these match
with de disorder of consciousness that occur in the late stages of dementia.
Is it true that people progress from the minimally conscious state to the
vegetative state before going into coma. I wonder if any research has been
done in this area, now that relatively simple techniques for detecting
conscious states have been discovered.
You should be here!
I finished reading the book
You should be here!
A book about Helsinki by Tom Bulgaria, which I started reading on
August 30 after I bought if on August 21.
I enjoyed reading this alternative tourist guide to Helsinki. It made me want
to stay there for some months and visit all the places mentioned in the book.
I stayed in Helsinki in May 1996.
PARR: corrections
While working on the counting algorithm for unique PARR configurations, I discovered an error in the
previously published results. The current
version of the program finds the results shown below in the table.
The bold number is the number of connected configuration in which not all
neighbour points have a connection and in which crossing diagonals are allowed.
| neighbours optional | neighbours connected |
| | crossing diagonals |
84,024,935,266,353,181
3,111,175,282,862,826 |
1,048,576
517,646 |
| no crossing diagonals |
4,147,603,839,035,069
82,280,232,154,141 |
2,976,416
2,041,600 |
When I biked home, I noticed, while biking on the Lonnekerbrugstraat, that the
sun behind a cloud just above the horizon was causing rays of light from above
and under the cloud. At the same time it started to rain a little, and when I
searched for a rainbow, I found a partial
(around 19:19). It quickly grew into an almost complete, rather faint single
rainbow. I waited for the sun to appear behind the cloud, hoping it would
result in a bright rainbow against al already rather dark background, but that
never happened. When around 19:23, I arrive at the end of the
Lonnekerbrugstraat my view was obstructed by some trees, and when I could see
the sky again, the rainbow was gone, and so where the rays because the sun had
disappeared behing some thick clouds. Later, I realized that this rainbow was
not caused by direct sunlight, which made it noteworthy.
Blao
This evening, Carina Schüring
visited us. She brought the painting, which she recently named 'Blao', with
her. It is the painting that I had decided to buy after we visited her on
Wednesday, July 15. After we had dinner, I
read through the purchase contract, stated in German, as she is a German
citizen, signed it, and transfered a sum of money to her account, thus making
me the owner of the work. The contract contained a clause, giving her the
right to put the work on display, whenever she has an exhibition, for which
it is suitable. I am very happy to borrow it to her for that purpose.
Book
At 10:15, I bought the book POPism: The Andy Warhol '60s by Andy
Warhol and Pat Hackett, from the charity shop
Het Goed for € 1.50.
Node.js
I uploaded a new version of the webiste
about Peter Struycken. This version has both static and dynamic parts. The
dynamic part is based on the JavaScript code, I
already had. The static part is generated with Node.js using the same data but with some additional files. Becaues it
seems that Node.js does not support a include mechanism, I wrote a batch file,
which just copies some files together. Because the website has both an English
and a Dutch part, and I basically need to run the same generation for two
languages, I came up with the idea to just include the generation part twice.
To reduce space, I already developed a small
program to strip JavaScript from useless information (spaces and comments)
and remove all data from 'src' fields in records. This is how the batch file
looks
Iparse.exe -s PS_js.gr dataSrc.js >errors.txt
StripJS.exe <dataSrc.js >data.js
StripJS.exe <enSrc.js >en.js
StripJS.exe <nlSrc.js >nl.js
StripJS.exe <contSrc.js >cont.js
StripJS.exe <dynSrc.js >dyn.js
more <data.js >temp.js
more <contSrc.js >>temp.js
more <enSrc.js >>temp.js
more <genSite.js >>temp.js
more <nlSrc.js >>temp.js
more <genSite.js >>temp.js
Node temp.js 2>>errors.txt
mysample.exe errors.txt
Unique PARR configurations
I completed the algorithm for finding unique PARR configurations. The algorithm makes use of the transition table
that is generated by the slicing method. It took me some time
to get all the rotations and mirrorings correct. The algorithm simply
generates all the configurations (up to a certain number of points) and then
rotates, mirrors the configuration in all directions seeing if it would result
in a 'smaller' configuration. If it does not, it is counted, and also written
to a binary file for later processing. With smaller, I mean that a binary
vector is made out of all the points and connections and if this vector is
smaller than the configuration in it original orientation. It appreared that
for the restriction that all pairs of neighbour points should have connection,
either with or without crossing diagonals, it is possible to calculate all
unique configurations within reasonable time. For the configurations where not
all neighbour points are connected, this is not feasable, simply because the
number connected configurations is more than a million times larger. Only all
unique configurations on nine or less points where counted and written to file.
The calculation for those configurations took almost six hours on
johan. I guess that for ten
or less points the time will more than fourty hours.
The current version of the program finds
the results shown in the table below. The numbers
between brackets are for all configurations with nine or less points.
| neighbours optional | neighbours connected |
| | crossing diagonals |
84,024,935,266,353,181
3,111,175,282,862,826
(17,682,852) |
1,048,576
517,646
113,346 |
| no crossing diagonals |
4,147,603,839,035,069
82,280,232,154,141
(10,215,753) |
2,976,416
2,041,600
466,446 |
The image shown with the
'PARR' bar on WLFR shows the
PARR 7|11 Reference Guide about PARR configurations with seven
points and eleven connections. The calculation show that there are a total of
802 connected PARR 7|11 configurations. The program PARRan_7_11.cpp when given the PARR_con_o_9.data file
as input produces the list of all solution (as ASCII art):
PARR_7_11.txt.
I just noticed that the image also shows a disconnected PARR on the left page
of the book that is layed open at the bottom half. Both PARR configuration
shown in that book have five points and four connections. I guess this is
the PARR 5|4 Reference Guide. Maybe I should also calculate the
number of unique configurations on disconnected PARR configurations.
PARR: maximal connections
When I was working on the PARR configurations,
I noticed that there were two unique configurations on five points with eight
connections. Because I could only imagine one such configuration, I first
thought that there must have been a bug in the program, but when I looked at
the print of the configurations, I found that five points in the shape of a
cross also have eight connections. Then, I began to look at the other
configurations with a maximal number of connections. I expected that there
would be a simple pattern in those, but that appeared not to be the case.
I found the following sequences of maximal number of connections for the
number of points starting with one: 1, 3, 6, 8, 11, 14, 17, 20, 23, 26, 30,
33, 36, 39, 43. I did check for this sequence in the The On-Line Encyclopedia of Integer Sequences®, but did not find it.
I made a drawing of all the maximal configurations on four to
sixteen points, in which red lines connect configurations of different sizes
that can be embedded without translation and a blue line for two configurations
that require mirroring:
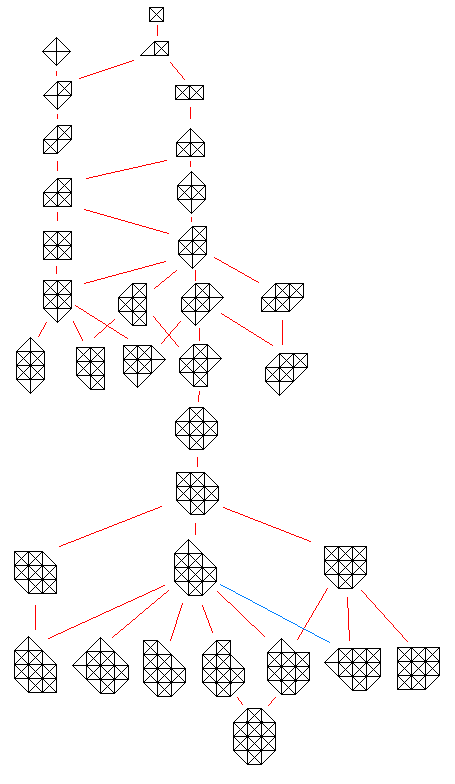
Remark: The second configuration on the second last row does not fit in
a 4 by 5 PARR configuration
Remark: The sequence has been added: Maximum number of intercardinal adjacencies among all n-celled polyplets
Home
| August 2015
| October 2015
| Random memories







