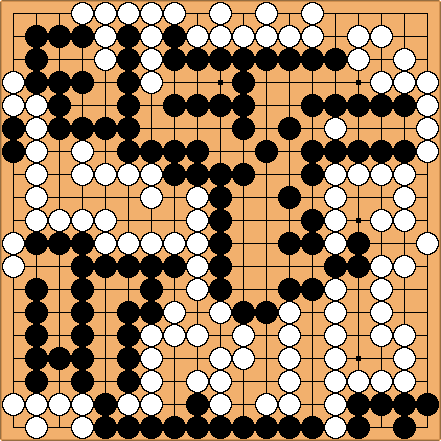
David Wolfe (link)
Experiments in Computer Go Endgames
by Martin Müller and Ralph Gasser
(PDF)
Generalized Thermography: Algorithms, Implementation, and Application to
Go Endgames
by Martin Müller, Elwyn Berlekamp,
and Bill Spight
(PDF)
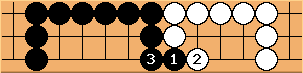
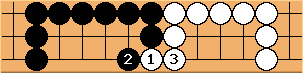
Miai counting
x + y = {xL + y, x + yL | xR + y, x + yR}
{ 0, 1, 2, 3, … | } = ω
{ 0 | 1, 1/2, 1/4, 1/8, … } = ε
π = {3, 25/8, 201/64, … | …, 51/16, 13/4, 7/2, 4}