Sun Mon Tue Wed Thu Fri Sat
1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
|
Amsterdam
I went by train to Amsterdam. Due to an accident, I was forced to take a detour
through Zutphen, which incured a delay of half an hour, and forced me having to
travel standing till Zutphen. I arived in Amsterdam around one o'clock. I took
the free ferry to the former N.D.S.M. shipyard. There I visited two art galeries. First I went to
Nieuw Dakota to see the Drawing
Front. I liked a drawing by Eline Lutz. Next, I visited Francis Boeske Projects to see the Untitled, 2016 exhibition. There were large painting by Oscar van der Put using bright and low saturated colour, or in other
words, almost white paintings.
I took the same ferry back to the central railway station and walked to
bookshop Scheltema where they were having a
sale. I walked through the whole shop and looked at hundreds of books. I bought
only two books:
After staying more than two hours in the bookshop, I walked back to the
central railway station, and I returned in Enschede around eight in the
evening.
Book
At 13:40:52, I bought the book Mijn generatie (in English: This
Generation) by Han Han
(韩寒), ISBN:9789029588423, from bookshop Broekhuis for € 5.00.
Our magnolia now is full with flowers. I guess that
about half of the flowers have opened. The first two flowers that opened
last week have turned brown. The tree also spreads
a strong fragrance in the garden.
Book
At 17:40, I bought the atlas De Bosatlas van
Amsterdam with Eelco Beukers as editor, ISBN:9789001120146, from V&D in
Enschede for € 14.50.
Street tiling patterns
This weekend, I continued working on the
program generating street tiling patterns. I have tried to eliminate
double patterns, but it seems there are still some in it. Below patterns with
area up to 20 unit squares can be viewed. These patterns do not have places
where four tiles (possibly of different sizes) touch in a corner. Also the
tiles are restricted to tiles of one by one, one by two, two by two, two by
three, and three by three. Patterns which contain a H (possible rotated by 90
degrees) are also excluded, which reduces the number of patterns considerably.
I also realized that some tiling patterns can be viewed as weave patterns. For
this all tiles used should have at least one side with unit length one. And
the one by one tiles should be assigned to either the horizontal or vertical
ribbons. And each ribbon should have a ribbon in the other direction going
under it. Preferable each colomn and row should have a ribbon. Under the
patterns that are excluded below, there are valid weave patterns.
Remark: The list of patterns has been corrected with results found on
April 13.
Book
At 11:35, I bought the book The Molyneux Problem by Irene Kopelman
edited by Moosje Goosen written in English published by Roma Publications on
Wednesday, January 30, 2013,
ISBN:9789077459881, from charity shop Het Goed
for € 1.75.
Street tiling patterns
I calculated the number of Street tiling
patterns for various restriction with latest version of the program to see if maybe some of the sequences are
included in The On-Line Encyclopedia of Integer
Sequences®. I did not discover any of them, which either means that
they contain errors or that nobody ever looked at them. The sequences are given
below, were each column gives the number of unique street tiling patterns with
respect to rotation and mirroring with stated area. The first row gives all
the sequences without restriction. This also contains sequences that repeat
themselves, thus have the same appearance as a sequence with an area that is a
fraction of the area. These are excluded in the second sequence. This sequence
still do contain points where four tiles meet (indicated with 'x') and that
contain H-shapes (indicated with 'H'), and where some of the vertices in the
H-shape might actually have four edges instead of the three that the H-shape
might suggest. The following sequences have additional restrictions on the
occurences of the number of tiles that meet in a point and the occurence of
H-shapes. The 's' signifies the additional restriction on the size of the
tiles, restricting them to one by one, one by two, two by two, two by three,
and three by three.
area 1,2,3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
--------------------------------------------------------------
all 1,4,6,24,25,98,93,386,520,1453,1749,8817,8398,30110,63789
xH 1,2,4,15,22,75,90,330,499,1375,1745,8507,8393,29825,63684
H 0,1,1, 5, 6,17,21, 59, 73, 172, 208, 633, 649, 1620, 2479
x 1,1,2, 5, 9,13,25, 39, 67, 114, 188, 401, 567, 1088, 1932
0,0,0, 1, 2, 3, 6, 9, 13, 24, 31, 59, 68, 126, 165
xH s 1,2,2, 9, 9,39,28,137,139, 447, 343,2163,1286, 5769, 8533
x s 1,1,1, 3, 4, 4, 8, 9, 17, 21, 28, 61, 63, 109, 156
H s 0,1,0, 2, 1, 4, 2, 9, 5, 14, 8, 40, 18, 49, 43
s 0,0,0, 1, 1, 0, 2, 1, 1, 2, 3, 6, 5, 5, 6
Hexagons
An observation related to the Four colour
theorem. Given two triangulations of a regular n-polygon. When these are
placed inside a regular 2n-polygon such that vertices of this polygon
alternatingly match with the vertices of the two n-polygons, then there can be
found exactly n-2 'empty' hexagons in the pattern of lines of the
triangulations of the polygons, where each hexagon consists of segments
altenately taken from the two triangulations. The proof for this is rather
simple. There must be a sequence of five vertices on the 2n-polygon, such that
v1, v3 and v5 hava a triangle in one of the
triangulations. There will also be a triangle attachted to vertices
v2 and v4. The third vertice, vi of this
triangle must be somewhere outside of the sequence. This is the only triangle
that 'crosses' the first triangle, and also the other way around. The two
'crossing' triangles have a (irregular) hexagon with alternating segments from
the two triangles. Now it is possible to construct two (n-1)-polygon with
triangluations by removing the two triangles. Removing the first triangle is
trivial because it is on the outside. To remove the second triangle, the
edges v2 to vi and v4 to vi have
to be merged. The various combinations for n equals six are shown on the top
right using the colours red and blue for the two triangulations. The four
hexagons are coloured white.
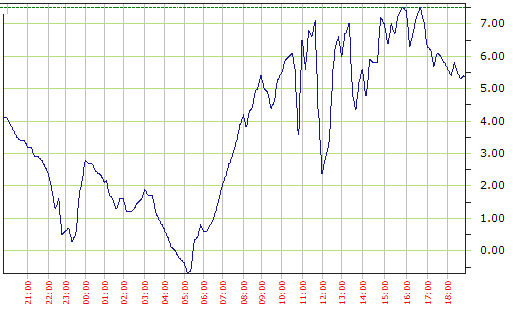
Hail and wet snow
Around eight in the morning, we had was a clear blue sky, which made me doubt
the weather report that we would get hail and (wet) snow. But around 10:50 there was hail. The sky cleared again. But then
again noon there was hail and also wet snow. And two hours later, again hail,
that even covered the ground for some time. The temperature has been rather
low for this time of the year. It is about 25 years ago, we had such low
temperatures at the end of April. Last night the temperature drop to -0.7°
Celsius. The highest temperature during the day, was just below seven degrees
Celsius. The temperature graph below, clearly shows the drops in the
temperature during the day that matched the periods of hail and wet snow. I
read that some soccer was aborted due to snow on the field around here.
Often when I write a program, I make use of a
simple single linked list to represent a mapping from keys to values.
Sometimes, I even do not bother about the list being sorted or stored in the
order the elements were added. Of course, there are containers available for
this in the Standard Template Library and Boost, but these require me to import the whole library. This afternoon,
I decided to implement a simple insert-only template for a program that I am
working on. The template class
InsertOnlyMap only has one method to find or insert a key to the
map. The method will return a pointer to the value for this key, which might
already have been present in the map or otherwise is added to it. Furhtermore,
it defines an iterator that can be used to iterate over the values in the map.
They key class should have a compare method, which return a integer
representing the compare result. A negative value will indicate that the value
is smaller than the one it is compared with and a positive value indicates that
it is larger. The implementation is based on a binary tree that is being
balanced on every insertion.
Das Logbuch / The Logbook
I received the book dOCUMENTA (13) : Das Logbuch / The Logbook 2/3,
which I bought for € 13.73 from bol.com. This to complete the set. I bought part 1/3 on
January 30 and part 3/3 on January 8.
This months interesting links
Home
| March 2016
| May 2016
| Random memories






 Magnolia
Magnolia